初三的同学们,学到相似三角形这一章,是不是感觉图形复杂,比例关系眼花缭乱?别怕!今天我们就来攻克相似模型中的“王牌基础”——A字型模型。掌握它,就如同拿到了破解一类几何难题的“万能钥匙”!
一、模型初窥:什么是“A字型”?
“A字型”模型,顾名思义,就是几何图形形状酷似英文字母“A”。它的核心在于 存在平行线 ,从而利用“平行线分线段成比例”定理或“相似三角形的判定”来建立线段之间的比例关系。
A字型模型主要分为三大类,让我们一起来认识一下。
模型一:构单A型相似(基础A字型)
这是最简单、最直接的A字型模型。
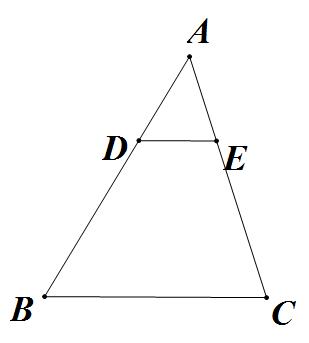
识别特征 :在三角形中,有一条线段与底边平行(即 )。
模型结论 :立刻可得 。
比例关系 :由此相似,我们可以得到一系列对应边成比例的关系,例如: 。
- 模型运用心法
- :只要在三角形内部看到平行线,基础A字型模型就“现身”了,直接应用相似结论即可。
模型二:构双A并排型相似(双A并行)
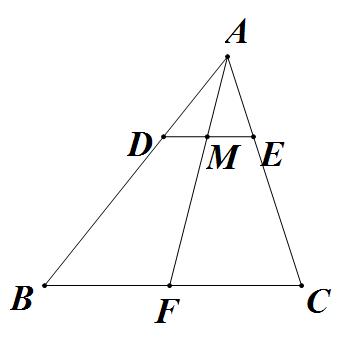
识别特征 :仍然有 ,但在此基础上,可能还有其它平行关系(如 , ),从而在大的A字型内部,嵌套了小的A字型。
模型结论 :存在多组相似三角形,如 , , 。
比例关系 :这些相似三角形共享一套比例关系,即 。这意味着,通过一条公共边的比例(如 ),可以连通整个图形中所有关键线段的比例。
例题1:构单A型相似
题目:
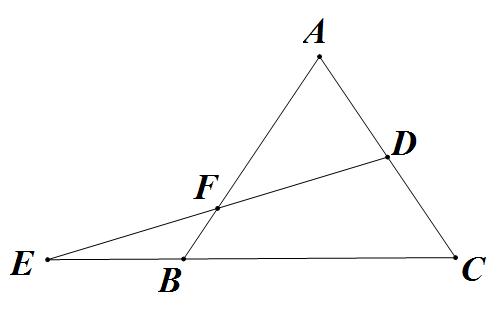
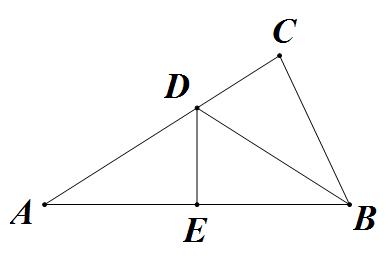
如图,在 中, 为边 的中点, 为 的延长线上一点,且 。 与 相交于点 。求 的值。
第一步:构造辅助线,搭建模型
由于图中没有直接可用的平行线,我们主动构造。
辅助线: 过点 作 ,交 于点 。
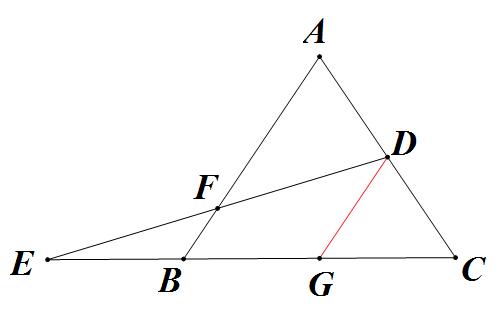
现在,图中出现了两个基本模型:
A字型相似:
1.在 中,因为 ,所以 。 2.在 中,因为 ,所以 。
第二步:利用模型建立比例关系
1. 利用A字型相似和已知条件:
由 得:
因为 是 中点,故 ,所以 ,即 为 中点,有 。
2. 利用A字型相似和已知条件:
由 得:
设 ,则 ,又 为 中点,故 ,得 ,所以 。代入(1)得:
3. 再次利用A字型相似求 :
由 得:
第三步:整合结果,求出答案
将(3)代入(2):
最终答案:
本题总结
解题关键在于“无中生有”:通过作平行线构造 A字型 的 相似模型,将中点与比例条件转化为目标线段比。逻辑清晰,模型典型,体现辅助线在几何解题中的核心作用。
好的,我们接着来详细解析例2。这道题是“构双A型相似”的典范,难度比例1有显著提升,更侧重于 利用角度条件证明平行关系 ,从而构造出模型。
例题2:构双A型相似
题目:
(1) 问题背景:
如图1,在 中,点 分别在 上, , ,求证: 。
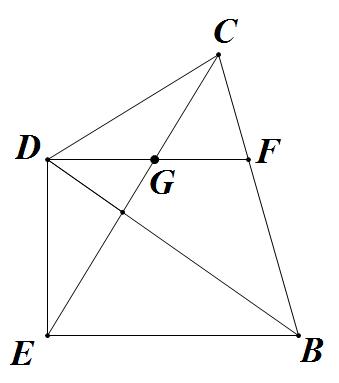
(2) 变式迁移:
如图2,在四边形 中, , , ,分别交 于点 。求证: 。
第(1)问证明:
因为 、 、 共线,所以 。
即: ...(1)
已知: ...(2)
由(1)和(2)可得:
两边减去 :
这意味着:** 平分 **,即 在 和 中:
( 平分 )
(已知 ,即 )
(公共边)
(ASA)
由全等可得:
第(2)问证明:
第一步:构造双A字型
延长 、 并使它们交于点 ,如图所示
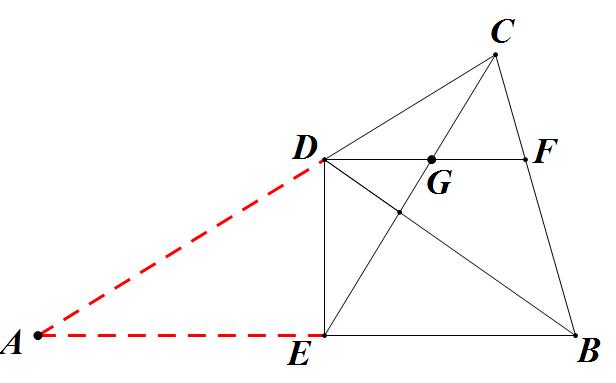
第二步:利用第(1)问的结论
由第(1)问,我们已经证明在 中,** 是 的中点**,即 。
第三步:构造第一组A字型相似(在△CEA中)
根据 平行于三角形一边的直线判定相似 ,我们有:
由这组相似,得到对应边成比例:
(1)
第四步:构造第二组A字型相似(在△CEB中)
根据相似判定,我们有:
由这组相似,得到对应边成比例:
(2)
第五步:连接比例,证明G是EF的中点
现在,我们得到了两个关于 的表达式。
由等式(1)和(2)可得:
第六步:利用中点E证明DG = FG(关键步骤)
已知 是 的中点,所以 。 因此可得: 。
有时候我们掌握了一些相似的基本模型会大大加快做题的效率,能快速识别或者构造出相似的三角形,例如在本文中的两道例题,可以通过构造平行,得出相似三角形从而解决问题




